Quelques règles de base à connaître pour additionner deux fractions
Si on multiplie (ou si on divise) le numérateur et le dénominateur d’une fraction par un même nombre entier non nul, on obtient une fraction équivalente.
Par exemple, si l’on multiple le numérateur et le dénominateur de la fraction 2/3 par 2, on obtient 4/6 qui est équivalente. Si on multiple le numérateur et le dénominateur par 3, on obtient 6/9 qui es toujours équivalente à 2/3.
Pour effectuer des additions entre des fractions, il faut qu’elles aient le même dénominateur.
On va donc s’arranger pour multiplier le numérateur et le dénominateur de chaque fraction jusqu’à ce que l’on obtienne le même dénominateur pour les 2 fractions à additionner.
Additionner des fractions qui ont déjà le même dénominateur
C’est le cas le plus facile, car il suffit d’additionner les numérateurs sans toucher au dénominateur. Vous trouverez (si vous avez de la chance) des questions avec deux fractions ayant déjà le même dénominateur à additionner dans les quiz sur OOXO.
Exemple : 23/15 + 7/15 = (23+7)/15 = 30/15.
30/15 est simplifiable car 30 = 2 x 15. Donc, en divisant haut et bas par 15, on obtient : 30/15 = 2.
Dans le quiz, les questions dont le résultat est simplifiable font partie des plus difficiles. Mais en jetant un oeil sur les 4 réponses proposées, vous verrez tout de suite le bon dénominateur.
[ads]
Additionner des fractions de dénominateurs différents
Cas le plus simple : les dénominateurs sont premiers entre eux
Pour additionner 2/3 et 3/5, on peut par exemple multiplier N et D (= numérateur et dénominateur) de la première par 5 pour obtenir 10/15, et N et D de la deuxième par 3 pour obtenir 9/15. On obtient ainsi 10/15 et 9/15 qui ont le même dénominateur, simplement en multipliant le dénominateur de l’une par le dénominateur de l’autre.
Donc, pour l’addition, on obtient : 10/15 + 9/15 = 19/15
On peut aussi rencontrer quelques cas particuliers
• L’un des dénominateurs est multiple de l’autre.
Exemple : 5/3 + 13/6.
On voit qu’au dénominateur : 6 = 3 × 2.
Donc, 6 est le dénominateur commun, et l’on peut écrire : (5×2)/(3×2) + 13/6 = 10/6 + 13/6 = 23/6 (non simplifiable).
• L’un des nombres est un entier (vous ne trouverez pas ce cas dans le quiz).
Exemple : 5 et 2/3.
3 est le dénominateur commun. On doit transformer 5 en une fraction ayant comme dénominateur 3 (comme l’autre fraction). On peut écrire : 5 = 5/1.
On multiplie donc haut et bas (numérateur et dénominateur) par 3 : (5 x 3)/(1 x 3) = 15/3
On obtient alors le résultat de l’addition : 15/3 + 2/3 = 17/3 (non simplifiable).
Mais on devra souvent calculer le PPCM
Hélas, tout n’est pas toujours aussi simple que dans les cas expliqués plus haut. Car si l’on veut additionner 17/12 et 5/24, on obtient (en multipliant bêtement les deux dénominateurs entre eux) 408/288 et 60/288. Et 408/288 + 60 /288 = (468 + 60)/288 = 528/288. On peut bien sûr simplifier en divisant par 2 le numérateur et le dénominateur : 264/144, et encore par 2 : 132/72, puis 66/36, et encore par 3 pour obtenir finalement 11/12. C’est un peu laborieux, car on manipule de grands nombres et on n’obtient pas le bon résultat de l’addition du premier coup d’une façon élégante.
La méthode recommandée pour réduire deux fractions au même dénominateur est la recherche du PPCM (plus petit commun multiple) des 2 dénominateurs, qui servira de dénominateur commun pour effectuer l’addition. Le PPCM est le plus petit entier strictement positif multiple de ces deux nombres.
De nombreux tutos existent sur internet pour expliquer et calculer le PPCM (voir les liens plus bas). Vous aussi trouver des infos sur Wikipédia : le PPCM. Nous ne reprendrons pas toutes les méthodes de calcul ici.
Exemple d’addition : 17/12 + 5/24
Cherchons le PPCM de 12 et 24. 12 = 2 x 2 x 3 et 24 = 2 x 2 x 2 x 3. Le PPCM est 24. Donc, on peut réduire 17/12 au même dénominateur que l’autre fraction en multipliant N et D par 2 : 17/12 = (17×2)/(12×2) = 34/24.
On peut maintenant calculer notre addition : 34/24 + 5/24 = 39/24. On peut simplifier le résultat en divisant N et D par 3. 39/24 = 13/8.
[ads]
Astuces pour faire l’addition mentalement dans les quiz OOXO
Deux méthodes de calcul mental
On peut soit calculer “brutalement” en multipliant les 2 dénominateurs et en simplifiant à la fin, soit deviner le PPCM, ce qui est facile car dans les quiz du site, les fractions à additionner ont un dénominateur compris entre 2 et 10.
Exemple : 9/4 + 7/2
• Calcul “brut” : on calcule le dénominateur commun en faisant 4×2 = 8. Puis on fait les produits 4×7 et 9×2 que l’on additionne : 28 + 18 = 46. On obtient le résultat 46/8 qui se simplifie en 23/4.
• Calcul plus subtil en devinant le PPCM : on voit que le PPCM des dénominateurs 4 et 2 est 4. On additionne donc 9/4 et (7×2)/(2×2), soit 9/4 + 14/4 = 23/4.
Pour réussir le quiz, il suffit d’apprendre par coeur les PPCM suivants. Ils correspondent aux nombres qui ne sont pas premiers entre eux. Seuls les 4 derniers sont moins évidents :
2 et 4 –> 4
2 et 6 –> 6 (ou 3 au dénominateur si le résultat se simplifie, ex : 5/2 + 7/6 = 11/3)
2 et 8 –> 8
2 et 10 –> 5
3 et 6 –> 6 (ou 2 au dénominateur si le résultat se simplifie, ex : 7/3 +7/6 = 7/2)
3 et 9 –> 9
4 et 6 –> 12
4 et 8 –> 8
4 et 10 -> 20
5 et 10 –> 10 (ou 2 au dénominateur si le résultat se simplifie, ex : 6/5 + 3/10 = 3/2)
6 et 8 –> 24
6 et 9 –> 18
6 et 10 –> 15
8 et 10 –> 40
C’est un peu comme en musique quand on entend des accords (avec des harmoniques en commun).
Le troisième quiz, qui présente des résultats dont le numérateur peut dépasser 100, est presque moins difficile que le deuxième. En effet, les dénominateurs sont toujours premiers entre eux et il suffit “bêtement” de les multiplier pour obtenir le dénominateur commun. De plus, toutes les réponses ont le même (bon) dénominateur. En utilisant la méthode décrite plus bas pour calculer le numérateur, on arrive vite à assimiler un mécanisme de calcul mental pour résoudre rapidement les 10 questions du quiz.
Comment “visualiser” les calculs ?
Dans les questions du quiz, les fractions sont écrites avec des “barres de division” (et pas avec des traits horizontaux qui auraient compliqué la rédaction).
On s’aperçoit vite que pour obtenir le numérateur du résultat, il suffit d’additionner les deux produits signalés par les flèches (verte et rouge) :
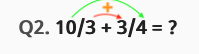 Dans ce cas, le numérateur du résultat est égal à (10×4) + (3×3) = 40 + 9 = 49. Le dénominateur commun est 3×4 = 12. Donc, le résultat est 49/12. On apprend vite à calculer de cette façon pour réussir les quiz en temps limité.
Dans ce cas, le numérateur du résultat est égal à (10×4) + (3×3) = 40 + 9 = 49. Le dénominateur commun est 3×4 = 12. Donc, le résultat est 49/12. On apprend vite à calculer de cette façon pour réussir les quiz en temps limité.
Lorsque les chiffres des dénominateurs communs ne sont pas premiers entre eux, on peut utiliser la même méthode puis simplifier à la fin, ou bien deviner le PPCM. Les cas les cas les plus faciles sont ceux avec des PPCM qui sont également un des deux dénominateurs (voir la liste ci-dessus).
Les cas moins faciles sont par exemple avec des dénominateurs 6 et 10 (PPCM = 15) ou 6 et 8 (PPCM = 24) qui demandent à faire plusieurs opérations mentalement.
Les cas les plus faciles sont dans le troisième quiz qui offre des additions de fractions avec des dénominateurs premiers entre eux. On peut donc faire une addition de 2 produits sans avoir à réfléchir pour obtenir le bon résultat. Exemple : 2/9 + 9/8 ? Dénominateur = 9×8 = 72 (tous les dénominateurs des réponses sont 72, on peut donc se passer du calcul !). Puis (9×9) + (2×8) = 81 + 16 = 97. Et voilà ! 97/72, réponse exacte. Avouez qu’en voyant ces grands nombres dans les fractions vous aviez un peu peur ! Et maintenant que vous connaissez cette astuce, vous pourrez épater la galerie ! Parfois, il y aura une retenue (ex : avec 7/6 + 8/7, on aboutit à 49 + 48 = 97), mais ce n’est pas un gros obstacle.
[ads]
Comment ont été créés et classés les quiz sur OOXO ?
Dans les 3 quiz proposés sur OOXO, les fractions à additionner ont un numérateur et un dénominateur inférieurs à 10. Vous trouverez donc 1/2 + 1/2, mais également des cas plus coriaces comme 3/10 + 7/6.
Tous les cas d’additions de 2 fractions (avec N et D <10) ont été créés de façon exhaustive, de 1/2 à 10/9, en ne gardant que les fractions irréductibles (N et D premiers entre eux). Par exemple seuls ont été sélectionnés 1/2, 3/2, 5/2, 7/2 et 9/2 pour les “demis” et 1/3, 2/3, 4/3, 5/3, 7/3 et 8/3 pour les “tiers”.
En tout, cela constitue une réserve de 2809 additions qui ont été classées en 4 catégories pour contenter tout le monde :
• Premier quiz (facile) : 779 cas avec des résultats dont le numérateur ou le dénominateur sont inférieurs à 20 ;
• Deuxième quiz (assez difficile) : 869 cas avec des résultats dont le numérateur ou le dénominateur sont compris entre 21 et 50 (parfois moins s’il y a simplification comme 46/24 = 23/12). Finalement ce quiz est parfois plus difficile que le troisième, car il faut simplifier le résultat. Le petit dénominateur du résultat est parfois un nombre plus élevé qu’il a fallu diviser par 2, 3 ou 4 si l’on effectue brutalement les calculs. Ce calcul brutal (produit des dénominateurs sans chercher le PPCM) et peut-être plus facile que de calculer le PPCM de tête. Les cas coriaces ont été extraits de ce quiz pur constituer le quatrième quiz (très difficile).
• Troisième quiz (difficile en apparence) : 1161 cas avec des résultats dont le numérateur ou le dénominateur sont supérieurs à 50. Seuls les amateurs avertis apprécieront des résultats comme 143/90 ou 151/63. En pratique, on s’aperçoit que de “grands” dénominateurs indiquent qu’il n’y a pas de simplification du résultat. Donc, le dénominateur du résultat est simplement le produit des 2 dénominateurs des fractions à additionner. Grands nombres, mais calcul mental relativement simple !
• Quatrième quiz (très difficile) : Parmi les 2809 fractions avec N ou D compris entre 1 et 10, 294 ont été sélectionnées soigneusement. Ce sont toutes celles dont la solution a un dénominateur différent des dénominateurs des 2 fractions à additionner. Bien sûr, le dénominateur de la solution ne sera pas le produit des dénominateurs des deux fractions à additionner ! Dans ce quiz, vous ne trouverez pas 1/2 + 1/2 = 1, ni 2/7 + 3/7 = 5/7, ni 7/8 + 5/9 = 35/72 ! Trop facile ! Il faudra à chaque fois effectuer plusieurs calculs, soit pour réduire au même dénominateur, soit pour simplifier le résultat.
Chaque quiz est composé de 10 questions tirées au sort parmi tous les cas retenus (779, 869, 1161 ou 294 selon le niveau). Le temps imparti pour répondre aux 10 questions est de 2 minutes. A vous de voir si vous vous prenez au jeu en vous lançant des défis, ou si vous voulez juste vous amuser 2 minutes…
[ads]
Calculateurs en ligne
• Calcul en ligne du plus petit dénominateur commun de plusieurs fractions
• Opérations sur les fractions (addition, soustraction, multiplication, division)
• Calculer en ligne le PPCM
• Calculer en ligne le PGCD
• Trouver les diviseurs d’un nombre entier
Tutos YouTube pour apprendre à additionner des fractions
• Addition de fractions dénominateurs différents
• Effectuer des additions et soustractions de fractions (niveau cinquième, partie 1/2)
• Effectuer des additions et soustractions de fractions (niveau cinquième, partie 2/2)
• Les fractions : Comment les mettre au même dénominateur (première partie)
• Les fractions : Comment les mettre au même dénominateur (deuxième partie)
• Mettre des fractions sur un dénominateur commun
• Additionner des fractions avec des dénominateurs différents
Articles et tutos sur les additions de fractions
• Les fractions : calculs et comparaisons (Open Classrooms)
• Trouver un dénominateur commun : Ce qu’il faut comprendre et retenir (Khan Academy)
• Wikipédia : les fractions
• Wikipédia : le PPCM